Introduction
We want to learn the concept "medium-built person" from examples.
We are given the height and weight of m individuals, the training set.
We
are told for each [height,weight] pair if it is or not of medium built.
We would like
to learn this concept, i.e. produce an algorithm that in the future
answers correctly if a pair [height,weight] represents/not a medium-built
person.
We are interested in knowing which value of m to use if we want to learn
this concept well.
Our concern is to characterize what we mean by well or good
when evaluating learned concepts.
First we examine what we mean by saying the probability of error of the learned concept is at most epsilon.
Say that c is the (true) concept we are learning, h is the concept we have learned, then
This method of evaluating learning is called Probably Approximately Correct (PAC) Learning and will be defined more precisely in the next section.
Our problem, for a given concept to be learned, and given epsilon and delta, is to determine the size of the training set. This may or not depend on the algorithm used to derive the learned concept.
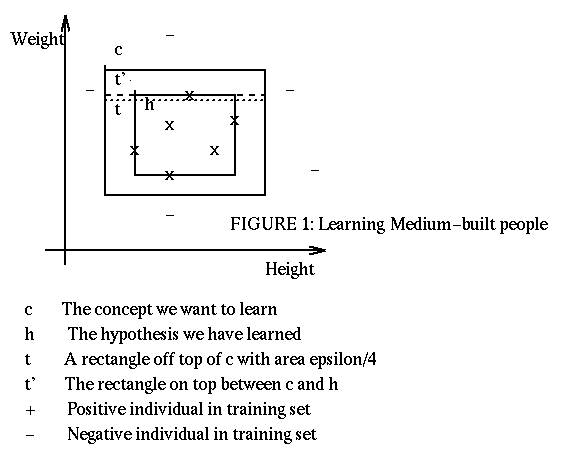
Going back to our problem of learning the concept medium-built people, we can assume that the concept is represented as a rectangle, with sides parallel to the axes height/weight, and with dimensions height_min, height_max, weight_min, weight_max. We assume that also the hypotheses will take the form of a rectangle with the sides parallel to the axes.
We will use a simple algorithm to build the learned concept from the training set:
We would like to know how good is this learning algorithm. We choose epsilon and delta and determine a value for m that will satisfy the PAC learning condition.
An individual x will be classified incorrectly by the learned concept h if x lays in the area between h and c. We divide this area into 4 strips, on top, bottom and sides of h. We allow these strips, pessimistically, to overlap in the corners. In figure 1 we represent the top strip as t'. If each of these strips is of area at most epsilon/4, i.e. is contained in the strip t of area epsilon/4, then the error for our hypothesis h will be bound by epsilon. [In determining the area of a strip we need to make some hypothesis about the probability of each point. However our analysis is valid for any chosen distribution.]
What is the probability that the hypothesis h will have an error bound by epsilon? We determine the probability that one individual will be outside of the strip t, (1 - epsilon/4). Then we determine the probability that all m individuals will be outside of the strip t, (1 - epsilon/4)^m. The probability of all m individuals to be simultaneously outside of at least one of the four strips is 4*(1 - epsilon/4)^m. When all the m individuals are outside of at least one of the strips, then the probability of error for an individual can be greater than epsilon [this is pessimistic]. Thus if we bound 4*(1 - epsilon/4)^m by delta, we make sure that the the probability of individual error being greater that epsilon is at most delta.
From the condition
Here are same representative values
epsilon | delta | m
=======================
0.1 | 0.1 | 148
0.1 | 0.01 | 240
0.1 | 0.001 | 332
-----------------------
0.01 | 0.1 | 1476
0.01 | 0.01 | 2397
0.01 | 0.001 | 3318
-----------------------
0.001 | 0.1 | 14756
0.001 | 0.01 | 23966
0.001 | 0.001 | 33176
=======================
It is not difficult, though tedious, to verify this bound.
One chooses a rectangle c, chooses values for epsilon and delta, and
runs an experiment with a training set of size m. One then
runs a test set and determines if the probability of error is
greater than epsilon.Here are some subcases of our problem of learning "rectangular concepts":
PAC Learning deals with the question of how to choose the size of the training set, if we want to have confidence delta that the learned concept will have an error that is bound by epsilon.
Formal Definition of PAC Learning
We set up the learning conditions as follows:
The error of an hypothesis h is defined as follows:
Lower Bound on the Size of the Training Set
Surprisingly, we can derive a general lower bound on the size m of the training set
required in PAC learning. We assume that for each x in the training set
we will have h(x) = f(x), that is, the hypothesis is consistent with the
target concept on the training set.
If the hypothesis h is bad, i.e it has an error greater than epsilon, and is consistent on the training set, then the probability that on one individual x we have h(x)=f(x) is at most (1 - epsilon), and the probability of having f(x)=h(x) for m individuals is at most (1 - epsilon)^m. This is an upper bound on the probability of a bad consistent function. If we multiply this value by the number of bad hypotheses, we have an upper bound on the probability of learning a bad consistent hypothesis.
The number of bad hypothesis is certainly less than the number N of hypotheses. Thus
Learning a Boolean Function
Suppose we want to learn a boolean function of n variables. The number N
of such functions is 2^(2^n). Thus
n | epsilon | delta | m =========================== 5 | 0.1 | 0.1 |245 5 | 0.1 | 0.01 |268 5 | 0.01 | 0.1 |2450 5 | 0.01 | 0.01 |2680 --------------------------- 10 | 0.1 | 0.1 |7123 10 | 0.1 | 0.01 |7146 10 | 0.01 | 0.1 |71230 10 | 0.01 | 0.01 |71460 ===========================Of course it would be much easier to learn a symmetric boolean function since there are many fewer functions of n variables, namely 2^(n+1).
We compute first the probability that a literal z is deleted from h
because of one specific positive example. Clearly this probability
is 0 if z occurs in c, and if ~z is in c the probability is 1. At issue are
the z where neither z nor ~z is in c. We would like to eliminate both of them
from h. If one of the two remains, we have an error for an instance a that is
positive for c and negative for h. Let's call these literals, free
literals.
We have:
Conclusions
Similar results have been obtained for a variety of learning problems,
including decision trees.
One has to be aware that the results on PAC learning are pessimistic. In practice smaller training sets than predicted by PAC learning should suffice.
Very interesting are the connections found between PAC learning and
Occam's Rasor. Occam's rasor gives preference to "simple" solutions.
In our context, "Occam Learning" implies that when learning concepts we
should give
preference to hypotheses that are simple, in the sense of being short
("short" is defined as a function of the shortest possible description
for the concept and the size of the training set).
It can be shown that under fairly general conditions an efficient
Occam Learning algorithm is also an efficient PAC Learning Algorithm.
References
Kearns,M.J.,Vazirani,U.V.: An Introduction to Computational Learning Theory, The MIT Press, 1994 Russell,S.J,Norvig,P.: Artifical Intelligence: A Modern Approach, Prentice-Hall, 1995 Dean,T.,Allen,J.,Aloimonos,Y.: Artificial Intelligence: Theory and Practice, The Benjamin/Cummings Publ.Co., 1995 Valiant,L.G.: A Theory of the Learnable, CACM, 17(11):1134-1142, 1984 CMU 15-681: Machine Learning: http://www-cgi.cs.cmu.edu/afs/cs.cmu.edu/user/avrim/www/ML94/courseinfo.html MIT 6.858: Machine Learning: http://theory.lcs.mit.edu/~mona/class94.html
ingargiola@cis.temple.edu