Introduction
Deadlock occurs when we have a set of processes
[not necessarily all the processes in the system], each holding some
resources, each requesting some resources, and none of them is able to
obtain what it needs, i.e. to make progress. We will usually reason
in terms of resources R1, R2, .., Rm and processes P1, P2, .., Pn.
A process Pi that is waiting for some currently unavailable
resource is said to be blocked.
Resources can be preemptable or
non-preemptable. A resource
is preemptable if it can be taken away from the process that is holding it
[we can think that the original holder waits, frozen, until the resource
is returned to it]. Memory is an example of a preemptable resource.
Of course, one may choose to deal with intrinsically preemptable resources
as if they were non-preemptable. In our discussion we only consider
non-preemptable resources.
Resources can be reusable or
consumable. They are reusable
if they can be used again
after a process is done using them. Memory, printers,
tape drives are examples of reusable resources. Consumable resources are
resources that can be used only once. For example a message or a signal
or an event.
If two processes are waiting for a message and one receives it, then the
other process remains waiting. To reason about deadlocks when dealing
with consumable resources is extremely difficult. Thus we will restrict our
discussion to reusable resources.
Resources are usually with a multiplicity,
i.e. an indication of how
many copies of the resource exist. So we may have 3 tape drives, 2 printers,
etc. We normally assume that resources have a multiplicity different than 1.
If it were always 1 the study of deadlocks could be simplified.
In fact, in the case of data bases, or of shared persistent objects, it is
usual to have only a single copy of the object (or if there are many copies,
as with replicated objects, their access from one user are so different
that we can treat the copies as distinct resources with multiplicity one).
Deadlock can only arise in a system where:
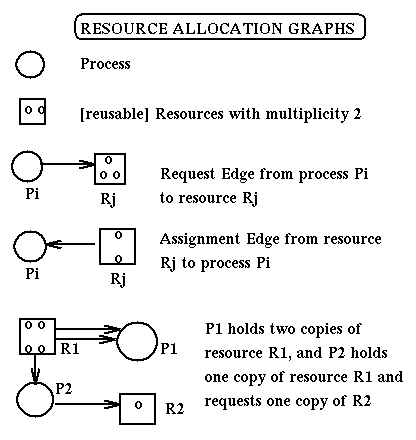
Resource Allocation Graphs
Resource Allocation Graphs (RAGs) are directed labeled
graphs used to represent,
from the point of view of deadlocks, the current state of a system.

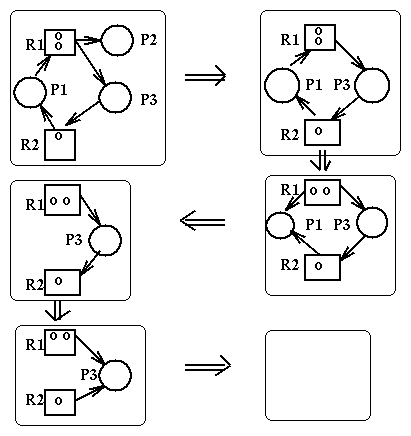
State transitions can be represented as transitions between the corresponding resource allocation graphs. Here are the rules for state transitions:
Here are some important propositions about deadlocks and resource allocation graphs:
Here is an example of reduction of a RAG:
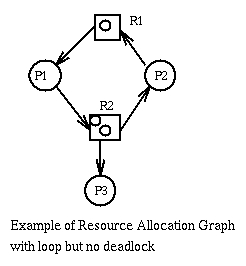
And here is a deadlock-free system with a loop.
Deadlock Prevention
Deadlock Prevention is to use
resources in such a way that we cannot
get into deadlocks. In real life we may decide that left turns are too
dangerous, so we only do right turns. It takes longer to get there but it
works. In terms of deadlocks, we may constrain our use of resources so that
we do not have to worry about deadlocks. Here we explore this idea with two
eaxmples.
It is easy to see that with this rule we will not get into deadlocks. [Proof by
contradiction.]
Here is an example of how we apply this rule. We are given a process that
uses resources ordered as A, B, C, D, E in the following manner:
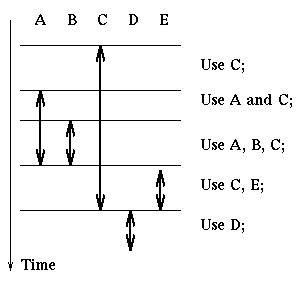
Then the process can do the following:
acquire(A); acquire(B); acquire(C);
use C
use A and C
use A, B, C
release(A); release(B); acquire(E);
use C and E
release(C); release(E); acquire(D);
use D
release(D);
A strategy such as this can be used when we have a few resources.
It is easy to apply and does not reduce the degree of concurrency too much.
Here is an example of use of this rule, locking a single resource at a time.
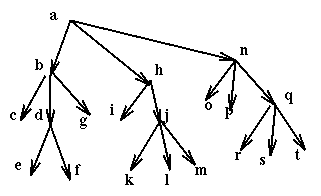
Then if a process wants to use the resources e, f, i, k it uses in sequence the commands:
Of course by forcing all locking sequences to start at the root of the resource hierarchy we create a bottleneck, since now the root becomes a scarce resource. As always there are trade-offs to be made. An obvious improvement on this prevention policy is to start not by locking the root, but by instead locking the lowest node subsuming all the nodes used by the current activity. For example if we had an activity that accessed only the nodes p, r, and s then we could start by locking n, not a.
Tannenbaum discusses prevention policies for distributed systems: the wait-die policy and the wound-wait policy, both based on the timestamp of competing transactions.
Deadlock Avoidance
Deadlock Avoidance, assuming that we are in a safe state
(i.e. a state from which there is a sequence of allocations and releases
of resources that allows all processes to terminate)
and we are requested certain resources, simulates the allocation of those
resources and determines if the resultant state is safe. If it is safe
the request is satisfied, otherwise it is delaied until it becomes safe.
The Banker's Algorithm is used to determine if a request can be satisfied. It uses requires knowledge of who are the competing transactions and what are their resource needs. Deadlock avoidance is essentially not used in distributed systems.
Deadlock Detection
Deadlock Detection, in the case where it is available information about
the full resource allocation graph, it is easy since there is deadlock
if and only if there is a loop in the resource allocation graph.
In the case that the multiplicity of resources is 1, we can simplify
the detection of deadlocks by building a wait-for graph, i.e
a graph where the nodes represent processes and there is an
arc from Pi to Pj if there is a resource R that is held by Pj and
requested by Pi. The wait-for graph of a system is always smaller than
the resource allocation graph of that same system.
There is a deadlock in a system if and only if there is a
loop in the wait-for graph of that system.
TRANSACTION T1 TRANSACTION T2 TRANSACTION T3
(Transfer from B (Transfer from (Transfer from A
to A and D) C to B) to C)
==============================================================
Lock(D)
Deposit to D
Lock(B)
Deposit to B
Lock(A)
Deposit to A
Lock(C)
Deposit to C
Lock(B)
Lock(C)
Lock(A)
---------------- Deadlock --------------------------------
Withdraw from B Withdraw from C Withdraw from A
Unlock A,B,D Unlock B,C Unlock A,C
===============================================================
we have the wait-for diagram
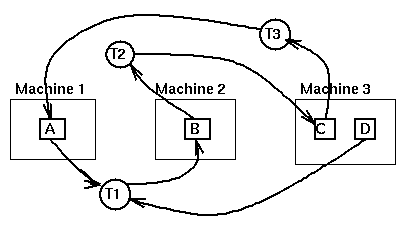
As Tanenbaum shows, when the wait-for graph is computed at a central
location that collects messages from the various systems involved
in transactions, it is easy to find also false, or spurious, or
phantom deadlocks as in the following picture
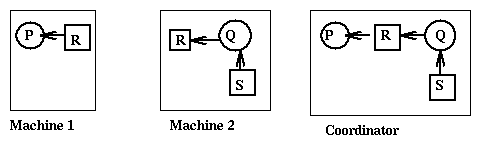
when Q first releases S and then P requests S, but the messages delivered
to the coordinator that collects the messages arrive in the wrong order.
Then the coordinator believes that a deadlock has arisen and kills
unnecessarily P or Q. Of course, if Q was following a 2-phase
locking policy, it would not release any lock until it had acquired
every lock it needed. Thus phantom deadlocks would not arise if
2-phase locking is followed.
The Chandy-Misra-Haas algorithm detects deadlocks in a distributed
system (resources with multiplicity 1) without requiring a coordinator.
When process Pi requests a resource held by process Pj, it
sends a message of form
[Requestor of resource,
source of message,
destination of message]
to Pj, thus in this case Pi sends to Pj the message [i, i, j].
In turn Pj will send to each process Ph such that Pj requests a
resource held by process Ph, the message [i, j, h]. The same
will be done by Ph, etc. if the original requestor Pi receives
a message of form [i, *, i], then it will know that there is a loop,
that a deadlock will arise, thus it will delay the request or abort.
For example, here is what happens in the following system
when process P1 requests a resource held by process P2:
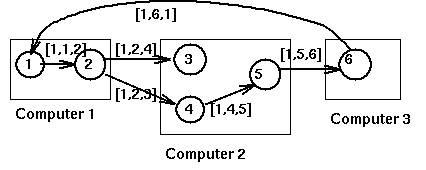
For distributed deadlock prevention can be used timestamps indicating the start of transactions and then ordering priority in case of conflictson the basis of the time stamp. The following diagram describes two deadlock prevention policies:
WAIT-DIE POLICY | WOUND-WAIT POLICY
|
Wants Holds | Wants
Resource Resource | Resource
+-------+ +-------+ | +-------+ +-------+
|Older |----->|Newer | | |Older |----->|Newer |
|Transac| |Transac| | |Transac| |Transac|
+-------+ +-------+ | +-------+ +-------+
It will wait | Preempt
|
|
Wants Holds | Wants Holds
Resource Resource | Resource Resource
+-------+ +-------+ | +-------+ +-------+
|Newer |----->|Older | | |Newer |----->|Older |
|Transac| |Transac| | |Transac| |Transac|
+-------+ +-------+ | +-------+ +-------+
It dies | It will wait